The series has been put on hold for now. I’m not happy with how the writing is going so for. There’s probably a better way to present the material that I need to think about.

The following list of posts in this series will be updated as I add more posts.

• Part 1: Levenshtein Distance and Delete Edits
• Part 2: Levenshtein Automata For Words

In the previous post, we looked at Levenshtein distances and proved a simple lemma about delete edits. Today we will look at Levenshtein automata for fixed words for a fixed maximal edit distance $k$. The automaton $A(p,k)$ will recognize all words $t$ that are at most $k$ distance away from $t$.

Some Terminology

We will use $\Sigma$ to denote the alphabet that characters of our strings come from. $\Sigma$ does not include the sentinel character $\$$.

For a character $c$, we will use the notation $q_0 \xrightarrow{c} q_1$ to denote a transition from the state $q_0$ to $q_1$ on input character $c$. $q_0 \xrightarrow{\Sigma} q_1$ will denote the set of transitions $\{q_0 \xrightarrow{c} q_1\,|\, c \in \Sigma\}$.

Levenshtein Automaton for a Fixed Word

Definition: The non-deterministic Levenshtein automaton $A(p,k)$ for a string $p=p_1 \cdots p_m$ with maximal edit distance $k$ is defined as follows.

1. The states of the automaton are $\{i^j\,|\,0 \leq i \leq m, 0 \leq j \leq k\}$. Note: $i^j$ is not exponentiation. It’s just syntax.
2. $0^0$ is the only start state.
3. The final states are $m^j$ for all $0 \leq j \leq k$.
4. The transitions are:
   • ${(i-1)}^j \xrightarrow{p_i} i^j$ (for matches).
   • $i^j \xrightarrow{\Sigma} i^{j+1}$ (for inserts).
   • $i^j \xrightarrow{\Sigma} {(i+1)}^{j+1}$ (for substitutions).
   • $i^j \xrightarrow{\varepsilon} {(i+1)}^{j+1}$ (for deletes).

Example: The figure below shows the automaton $A(\texttt{abac},2)$.

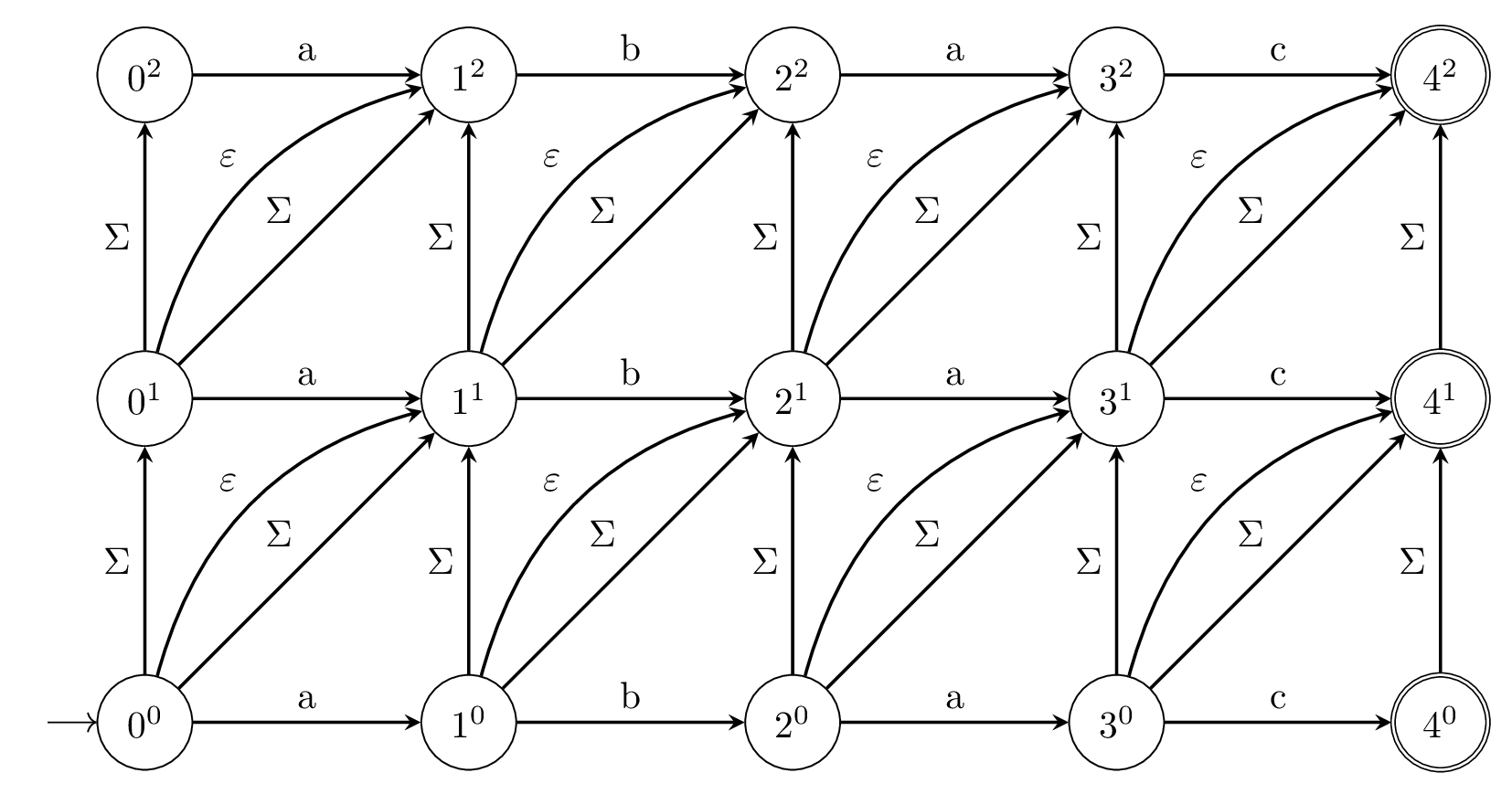
It is easy to see that any path from $0^0$ to $4^j$ into a stream of matches and character edits and that the atomaton allows for at most $2$ character edits. Rigorous proofs of this can be found in the literature.

Removing Epsilon Transitions

Using the lemma about delete edits from the previous post, we can easily remove the epsilon transitions. We simply replace the epsilon transitions with the following and add some additional final states.

• ${(i-l-1)}^j \xrightarrow{p_i} i^{j+l}$ (for deletes).

We add the states from which we could traverse to some $m^j$ via epsilon transitions to the set of final states.

• The final states are ${(m-l)}^j$ for all $0 \leq j,l \leq k$ where $j+l \leq k$.

Example: The figure below shows the automaton for abac with $k=2$ without epsilon transitions.

Single Column of Final States

For removing epsilon transitions, we had to add additional final states in case the input text was too short. We can go back to final states being in a single column if we use the sentinel character to signal the end of the text and the end of the input.

For simplicity, we extend the alphabet to $\Sigma' = \Sigma \cup \{\$\}$. We will add some additional states $(m+1)^{j}$ for $0\leq j \leq k$.

Given an input string $t$ of length $n \leq m + k$, we will feed extra $\$$ characters to the automaton till we have fed exactly $m + k$ characters.

Example: The figure below shows the automaton for abac with $k=2$ without epsilon transitions which allows for the sentinel character as an input.