This post assumes familiarity with the Rc<RefCell<...>> type in Rust. The Red-Black Tree parts aren’t specific to Rust, but some of pointer dereferencing is a bit awkward because we’re using Rc<RefCell<...>>.

I’ve been taking another look at Rust. I read the Rust Book, and then have been implementing some data structures which led me to implement Red-Black Trees. Going through the Red-Black Tree implementation in CLRS, I was very unsatisfied with the repeated code with the symmetric cases. In the different cases, there’s a bunch of code first figuring out which child of a parent a given node is and then acting accordingly. This felt counterproductive to me since we could have precomputed this while creating the tree. The pre-computation uses some additional space, but Red-Black Trees already use some additional space for the Color, so it feels harmless. If there’s some extra space left in the Node struct after storing Color, we might not even need extra space.

We start with defining the Node type.

type BareTree<K, T> = Rc<RefCell<Node<K, T>>>;
type Tree<K, T> = Option<BareTree<K, T>>;

pub struct Node<K: Ord, T> {
    color: Color,
    key: K,
    value: T,
    parent: Tree<K, T>,
    child_of_parent: Option<RBSide>,
    left: Tree<K, T>,
    right: Tree<K, T>,
}

Here, the only addition compared to a standard implementation is the child_of_parent field. This field is used to store whether the node is a left child or a right child.

We’re going to need some primitive operations on Nodes: set_parent, set_child, take_child, and get_child.

impl<K, T> Node<K, T> {
    fn get_child(&self, child: RBSide) -> Tree<K, T> {
        match child {
            RBSide::Left => self.left.clone(),
            RBSide::Right => self.right.clone(),
        }
    }

    fn take_child(&mut self, child: RBSide) -> Tree<K, T> {
        match child {
            RBSide::Left => self.left.take(),
            RBSide::Right => self.right.take(),
        }
    }

    fn set_parent(&mut self, child_of_parent: RBSide, parent: BareTree<K, T>) {
        self.parent = Some(parent);
        self.child_of_parent = Some(child_of_parent);
    }

    fn set_child(&mut self, side: RBSide, child: Tree<K, T>) {
        match side {
            RBSide::Left => self.left = child,
            RBSide::Right => self.right = child,
        }
    }
}

They all take an RBSide parameter. This is what allows us to share the code between the different symmetric cases in Red-Black Tree. Instead of rewriting code for left and right cases, we implicitly act on the correct case using RBSide. The set_parent and set_child are shallow operations, setting the child does not automatically set the parent of that child. The take_child sets the child field to None when fetching the child.

The code for adding a node to a tree is similar to regular Red-Black Trees, but still benefits from code sharing between the symmetric cases. We simply get which direction to go down, and then string together take_child, a recursive call, a set_parent, and a set_child. A difference from the regular adding for Red-Black Trees, the set_parent calls set the child_of_parent field as we are recurse down the tree.

pub struct RBTree<K: Ord, T> {
    root: Tree<K, T>,
}

impl<K: Ord + Copy, T: Clone> RBTree<K, T> {
    pub fn add(&mut self, key: K, value: T) {
        let root = self.root.take();
        let (_new_rooted, new_node) = self.add_r(root, key, value);
        self.root = self.fix_tree(new_node)
    }

    fn insert_side(&self, subroot_key: K, insert_key: K) -> RBSide {
        if subroot_key <= insert_key {
            RBSide::Right
        } else {
            RBSide::Left
        }
    }

    fn add_r(&mut self, node: Tree<K, T>, key: K, value: T) -> (BareTree<K, T>, BareTree<K, T>) {
        match node {
            None => {
                let new = Node::new(key, value);
                (new.clone(), new)
            }
            Some(n) => {
                let current_key = n.borrow().key;
                let insert_side = self.insert_side(current_key, key);

                // Insert into insert_side
                let old_child_subtree = n.borrow_mut().take_child(insert_side);
                let (new_child_subtree, inserted_node) = self.add_r(old_child_subtree, key, value);

                new_child_subtree
                    .borrow_mut()
                    .set_parent(insert_side, n.clone());
                n.borrow_mut()
                    .set_child(insert_side, Some(new_child_subtree));
                (n, inserted_node)
            }
        }
    }
}

After an insert, to restore the red-black tree properties, we must fix recursively balance any red-red edges or the color the root red if it’s black. This is the job of the RBTree::fix_tree function, which relies on two helper functions, RBTree::uncle and RBTree::rotate.

RBTree::uncle not only gets the uncle node, but also which side of the grand parent the uncle lies on. Because we precomputed which side of the grandparent node we start from, getting to the uncle node is vastly simplified. In the code below, most of the lines are just there for dereferencing through &Rc<RefCell<...>>.

    // should only be called nodes where the parent is red, i.e. grand parent exists
    fn uncle(&self, node: &BareTree<K, T>) -> (RBSide, Tree<K, T>) {
        let node_ref = node.borrow(); 
        let parent = node_ref.parent.as_ref().unwrap();
        let parent = parent.borrow();
        let other_side = parent.child_of_parent.unwrap().other();
        let grand_parent = parent.parent.as_ref().unwrap();
        let uncle = grand_parent.borrow().get_child(other_side);
        (other_side, uncle)
    }

RBTree::rotate rotates the subtree at parent and assumes that there’s a non-None child on child_side. We don’t have to write separate code for left and right rotations, and just use the single function for both kinds of rotation, just passing the direction where the child node is.

    fn rotate(&self, child_side: RBSide, parent: BareTree<K, T>) {
        let mut parent_mut = RefCell::borrow_mut(&parent);
        let other_side = child_side.other();

        let child_rc = parent_mut.get_child(child_side).unwrap();
        {
            // scope for borrowing child_rc
            let mut child = RefCell::borrow_mut(&child_rc);

            let grand_parent = parent_mut.parent.take();
            let child_of_grand_parent = parent_mut.child_of_parent.take();
            if let Some((gp, c)) = grand_parent.as_ref().zip(child_of_grand_parent) {
                gp.borrow_mut().set_child(c, Some(child_rc.clone()));
            }

            let grand_child = child.take_child(other_side);
            if let Some(gc) = grand_child.as_ref() {
                gc.borrow_mut().set_parent(child_side, parent.clone())
            }
            parent_mut.set_child(child_side, grand_child);

            child.parent = grand_parent;
            child.child_of_parent = child_of_grand_parent;
            child.set_child(child_side.other(), Some(parent.clone()));
        }
        parent_mut.set_parent(other_side, child_rc);
    }

We finally come to to RBTree::fix_tree. The only violations are that the root is red or there are red-red edges. The cases for red-red edges are as follows:

1. The uncle node is Red. In this case we color the grandparent Red, color the uncle and parent Black, and recurse on the grandparent.
2. The uncle node is Black. This case boils down to two cases.
   1. The parent is on one side of the grandparent, but the node is on a different side of the parent. For this case, we rotate to reduce to case b.
   2. Node-parent is same as parent-grandparent. The grandparent is Black. We rotate on the grandparent to make a subtree rooted at parent, with the current node and grandparent node as its children. The color of the parent node is changed from Red to Black, the color of the grandparent is changed from Black to Red, and the color of the current node stays Red.

    fn fix_tree(&mut self, inserted: BareTree<K, T>) -> Tree<K, T> {
        let mut not_root = inserted.borrow().parent.is_some();
        let root: BareTree<K, T> = if not_root {
            let mut n: BareTree<K, T> = Rc::clone(&inserted);
            let mut parent_is_red = self.parent_color(&inserted) == Color::Red;
            // n is red
            while parent_is_red && not_root {
                // parent_is_red implies grand_parent exists and is black
                let (uncle_side, uncle) = self.uncle(&n);
                let mut parent = n.borrow().parent.as_ref().unwrap().clone();
                if uncle.is_some() && uncle.as_ref().unwrap().borrow().color == Color::Red {
                    // uncle red
                    let uncle = uncle.unwrap();
                    parent.borrow_mut().color = Color::Black;
                    uncle.borrow_mut().color = Color::Black;
                    let grand_parent = parent.borrow().parent.as_ref().unwrap().clone();
                    grand_parent.borrow_mut().color = Color::Red;
                    n = grand_parent;
                } else {
                    // uncle is black
                    let parent_side = uncle_side.other();
                    let node_side = parent.borrow().child_of_parent.unwrap();
                    if node_side != parent_side {
                        // rotate to make parent of child of node
                        self.rotate(node_side, parent.clone());
                        {
                            let temp = parent;
                            parent = n;
                            n = temp;
                        }
                    };
                    // parent (currently red) will replace black grand_parent
                    parent.borrow_mut().color = Color::Black;
                    let grand_parent = RefCell::borrow(&parent).parent.clone().unwrap();
                    grand_parent.borrow_mut().color = Color::Red;
                    self.rotate(parent_side, grand_parent);
                }
                not_root = n.borrow().parent.is_some();
                parent_is_red = not_root && { self.parent_color(&n) == Color::Red }
            }
            while not_root {
                let temp = n.borrow().parent.clone().unwrap();
                not_root = temp.borrow().parent.is_some();
                n = temp;
            }
            n
        } else {
            inserted
        };
        RefCell::borrow_mut(&root).color = Color::Black;
        Some(root)
    }

    // only called on non-root (red) nodes, so parent can be unwrapped
    fn parent_color(&self, node: &BareTree<K, T>) -> Color {
        let node_ref = node.borrow();
        let parent = node_ref.parent.as_ref().unwrap();
        let parent_ref = parent.borrow();
        parent_ref.color
    }

Notice that in the above implementation, there is no repeated code for the symmetric cases. For the sake of completion, the Color and RBSide types are as follows.

enum Color {
    Red,
    Black,
}

enum RBSide {
    Left,
    Right,
}

impl RBSide {
    fn other(self) -> Self {
        match self {
            RBSide::Left => RBSide::Right,
            RBSide::Right => RBSide::Left,
        }
    }
}

The full code for this post is available here.

The series has been put on hold for now. I’m not happy with how the writing is going so for. There’s probably a better way to present the material that I need to think about.

The following list of posts in this series will be updated as I add more posts.

• Part 1: Levenshtein Distance and Delete Edits
• Part 2: Levenshtein Automata For Words

In the previous post, we looked at Levenshtein distances and proved a simple lemma about delete edits. Today we will look at Levenshtein automata for fixed words for a fixed maximal edit distance $k$. The automaton $A(p,k)$ will recognize all words $t$ that are at most $k$ distance away from $t$.

Some Terminology

We will use $\Sigma$ to denote the alphabet that characters of our strings come from. $\Sigma$ does not include the sentinel character $\$$.

For a character $c$, we will use the notation $q_0 \xrightarrow{c} q_1$ to denote a transition from the state $q_0$ to $q_1$ on input character $c$. $q_0 \xrightarrow{\Sigma} q_1$ will denote the set of transitions $\{q_0 \xrightarrow{c} q_1\,|\, c \in \Sigma\}$.

Levenshtein Automaton for a Fixed Word

Definition: The non-deterministic Levenshtein automaton $A(p,k)$ for a string $p=p_1 \cdots p_m$ with maximal edit distance $k$ is defined as follows.

1. The states of the automaton are $\{i^j\,|\,0 \leq i \leq m, 0 \leq j \leq k\}$. Note: $i^j$ is not exponentiation. It’s just syntax.
2. $0^0$ is the only start state.
3. The final states are $m^j$ for all $0 \leq j \leq k$.
4. The transitions are:
   • ${(i-1)}^j \xrightarrow{p_i} i^j$ (for matches).
   • $i^j \xrightarrow{\Sigma} i^{j+1}$ (for inserts).
   • $i^j \xrightarrow{\Sigma} {(i+1)}^{j+1}$ (for substitutions).
   • $i^j \xrightarrow{\varepsilon} {(i+1)}^{j+1}$ (for deletes).

Example: The figure below shows the automaton $A(\texttt{abac},2)$.

It is easy to see that any path from $0^0$ to $4^j$ into a stream of matches and character edits and that the atomaton allows for at most $2$ character edits. Rigorous proofs of this can be found in the literature.

Removing Epsilon Transitions

Using the lemma about delete edits from the previous post, we can easily remove the epsilon transitions. We simply replace the epsilon transitions with the following and add some additional final states.

• ${(i-l-1)}^j \xrightarrow{p_i} i^{j+l}$ (for deletes).

We add the states from which we could traverse to some $m^j$ via epsilon transitions to the set of final states.

• The final states are ${(m-l)}^j$ for all $0 \leq j,l \leq k$ where $j+l \leq k$.

Example: The figure below shows the automaton for abac with $k=2$ without epsilon transitions.

Single Column of Final States

For removing epsilon transitions, we had to add additional final states in case the input text was too short. We can go back to final states being in a single column if we use the sentinel character to signal the end of the text and the end of the input.

For simplicity, we extend the alphabet to $\Sigma' = \Sigma \cup \{\$\}$. We will add some additional states $(m+1)^{j}$ for $0\leq j \leq k$.

Given an input string $t$ of length $n \leq m + k$, we will feed extra $\$$ characters to the automaton till we have fed exactly $m + k$ characters.

Example: The figure below shows the automaton for abac with $k=2$ without epsilon transitions which allows for the sentinel character as an input.

My recent discovery of (Non-deterministic) Universal Levenshtein Automata (NULA) have been really engaging creatively. In this series of posts, I am going to collect together some definitions, theorems, and proofs about Levenshtein Distances and NULAs, and then provide a second set of definitions so that we can use bitwise operations for the implementation of NULAs.

The series has been put on hold for now. I’m not happy with how the writing is going so for. There’s probably a better way to present the material that I need to think about.

The following list of posts in this series will be updated as I add more posts.

• Part 1: Levenshtein Distance and Delete Edits
• Part 2: Levenshtein Automata For Words

Levenshtein Distance

Definition: The Levenshtein Distance between two strings is the minimal number of character edits required to change one string into the other. A character edit is inserting a character, deleting a character, or substituting a character for another.

Example: The Levenshtein distance between "abc" and "abd" is 1. The character edit substitutes 'c' with 'd'.

Example: The Levenshtein distance between "abc" and "abdc" is 1. The character edit inserts 'd' before 'c'.

Example: The Levenshtein distance between "abc" and "ac" is 1. The character edit delete the 'b'.

Example: The Levenshtein distance between "abc" and "acd" is 2. There are a few ways of doing two edits to "abc" to get "acd". One way is to substitute the 'b' for 'c' and the 'c' for 'd'. Another way is to delete the 'b' and insert the 'd'. This shows that the character edits involved need not be unique.

In some areas of applications, it is useful to consider more kinds of edits. For example, in spell checking inputs from a keyboard, you might consider swapping two adjacent characters (transpositions) as an edit, and in optical character recognition you might consider splitting one character into two and merging two characters into one as edits.

Some Terminology

Let $t$ be a string of length $n$. We will represents the $i$-th character of $t$ as $t_i$. So $t = t_1 t_2 \cdots t_n$.

We will represent character edits as follows.

1. Substituting the $i$-th character will be represented as $s_i$.
2. Deleting the $i$-th character will be represented as $\varepsilon_i$.
3. An insert edit will be represented as $i_k$, where $k$ is the $k$-th insert edit.

We will not use $s$ or $i$ for strings, and it will be clear from context whether we are using $i$ as an index or as an insert edit.

We will use $\$$ as a sentinel character when needed, often to represent the end of strings. Replacting $\$$ will not be allowed for substitution edits.

Example: Let $t$ be the string "abc". Then $t_1$ = 'a', $t_2$ = 'b', and $t_3$ = 'c'. One way of minimally editing $t$ to get "acd" can be represented as $t_1 s_2 s_3$, where $s_2$ = 'c' and $s_3$ = 'd'. Another way of minimally editing $t$ to get "acd" can be represented as $t_1 \varepsilon_2 t_3 i_1$, where $i_1$ = 'd'.

A Lemma About Delete Edits

Lemma: Let $p$ and $t$ be two strings. Given a set of minimal character edits to transform $p$ to $t$, we can rearrange the edits so that every maximal sequence of delete edits are followed by a character match or are at end of the string.

Proof: We will shift maximal sequences of delete edits to the right till they are followed by a character match or they are at the end of the string.

Suppose we have the sequence $\varepsilon_k \varepsilon_{k+1} \cdots \varepsilon_{k + j} i_n$ in $t$, i.e. we are deleting $j$ characters starting at character $p_k$ and then inserting a character. This can be rewritten as $i_n \varepsilon_k \varepsilon_{k+1} \cdots \varepsilon_{k + j}$. This changes the edits so that we are inserting a character first, and then deleting $j$ characters starting at $p_k$.

Suppose we have the sequence $\varepsilon_k \varepsilon_{k+1} \cdots \varepsilon_{k + j} s_{k + j + 1}$ in $t$ with $s_{k + j + 1} \neq p_{k + j + 1}$. Here we are deleting $j$ characters starting at character $p_k$ and then substituting the $k+j+1$-th character. This can be rewritten as $s_{k} \varepsilon_{k+1} \varepsilon_{k+2} \cdots \varepsilon_{k + j + 1}$. This changes the edits so that we are substituting the $k$-th character, and then deleting $j$ characters starting at $p_{k+1}$. Note that $s_k$ cannot equal $p_k$ since that would mean we found a smaller set of edits than the minimal set of edits we started with.

The above two steps can be repeated for maximal sequences of delete edits in $t$ until all maximal sequences of delete edits are followed by a match $p_k$ or are at the end of the string. $\square$

Update We do not need to worry about delete edits followed by a transposition. A delete followed by a transposition is two edits, but so is a substitution followed by a match followed by a delete. If our string is $t$ = abc, and we are matching with cb, we can write cb as $s_1 t_2 \varepsilon_3$. Longer delete sequences followed by a transposition $\varepsilon_i \varepsilon_{i+1} \cdots \varepsilon_{i+k} t_{i+k+2} t_{i+k+1}$, can be similarly thought of as $\varepsilon_i \varepsilon_{i+1} \cdots \varepsilon_{i+(k-1)} s_{i+k} t_{i+k+1} \varepsilon_{i+k+2}$, where $s_{i+k} = t_{i+k+2}$.

I recently fixed a time out issue in SWAN, the static analysis framework for Swift that our lab works on. The algorithm was a fixpoint style algorithm, where the same work items are worked on over and over again until no new information in generated. For the particular issue that I fixed, I spent a lot of time chasing after the hypothesis that some work items were being unnessarility being revisited over and over again. This turned out not to be the case. Below I will describe some of the reasons why I had the hypothesis in the first place, and how I got out of the loop to find the actual issue.

Let’s start off with the issue we were having in SWAN. We were trying to analyze some open source projects, and for many of them, we were timing out during call-graph construction. A call-graph is a directed graph where the nodes are methods in a program and there is a edge from a method A to a method B if A calls B. For languages with only static dispatch (e.g. C without function pointers), this graph is very easy to construct — to check if there should be an edge from A to B, we can just check if B shows up as a callee in A’s body. But in languages with dynamic dispatch or function pointers, to check if A calls B, we must check if there is a callee in A’s body that can resolve to B dynamically.

SWAN uses an RTA [1] style call-graph construction algorithm where keep track of the classes and protocols that have been instantiated by the program and only draw edges to methods of those classes and protocols for dynamic dispatches. The fixpoint parts of the algorithm show up when, while analyzing a method, we find instantiations of a new class (or protocol). If such a class is found, we muct revisit all methods and draw edges to methods of this new class. Further, visiting this new class’s methods can lead to the discovery of more classes/protocols which can lead to more revisiting of already visited methods of the program.

Now, to the problem at hand: time outs! I picked a project that SWAN was timing out on and ran SWAN with a debugger on it. During call-graph construction I paused SWAN at certain points to see what methods were being visited by SWAN at that point. For the most part, whenever I paused, SWAN was visiting the same group of methods. I had some logs showing that I was pausing at different runs on those methods, so the algorithm was not just stuck on the same method for a very long time. This is what lead me to believe that we were probably revisiting the same method over and over again.

At this point, I considered two main possibilities. Either the code that checks to see if new information has been generated is buggy, or the code that generates new information is generating faulty new information. I manually inspected the code to find the places where the checks were happening. This took some time, but there seemed to be nothing wrong with the checks. Throughout the next few steps, I would return to the checks just to be sure. And at one point even convinced myself that the checks were faulty, but I turned out to be wrong.

Checking for faulty new information was more difficult. There were lots of places where new information was potentially being generated. I tried to log the information that was being generated, but it quickly started to generate unreadable logs. Plus what counted as faulty information was not clearly defined, so I could not write logging code to only log when faulty information was being generated. I would run SWAN, it would keep running without generating anything useful in the logs.

Next, I started logging runtimes for different parts of the program. The first step of the call-graph algorithm takes in a list of entry points to a Swift program, and it traverses blocks of methods reachable from those entry points while keeping a list of instantiated types (classes and protocols). The entry points are processed more or less independently, so I started timing processing times for different entry points. SWAN considers any uncalled function to be an entry point, and there were around 12000 entry points for the project I was looking at. Looking at the logs, it looked like, most entry points took almost no time at all to process, but then SWAN would get stuck on one entry point before I killed it.

Luckily, among the entry points that SWAN would successfully complete before I killed it, I found one entry point that took about 5 minutes (~ 300 seconds). I hardcoded SWAN to only process this single entry point, and then started logging the methods that were being visited. I could still see that some methods were being revisited several times. I was still working with the hypothesis that these methods were being visited more often that they should be, so I started looking at, why they are being revisited. At first I tried to manually inspect the Swift code, but turned out to be pretty hairy, and I gave up on that approach pretty quickly. Then I tried to look at why the methods were being revisited.

As I had checked earlier, the methods were being revisited because new instantiated types were being discovered. Fortunately, the instantiated types were stored as a set of strings, making it very easy to hard code. When I hardcoded this set of strings into the algorithm, methods were being visited only once, but the performance of the algorithm improved by only 30 to 50 percent. At this point, I finally gave up on my hypothesis that methods were being unnecessarily revisited.

For every module of the program it is analyzing, SWAN creates what it calls a dynamic dispatch graph (DDG). A DDG keeps track of possible resolutions to dynamic references, and the call-graph algorithm performs some reachability queries on this graph. In some of my previous tests, when I was randomly pausing SWAN at different points, a few of the times, the program paused in the middle of a DDG query. I added some timers to log whenever a DDG query took more than 2 seconds, and in the entry point I was testing, there were around 5 queries that took more than 2 seconds and they each took about 5 seconds. From those times, the long queries could not really explain the 5 minutes it took to construct the call-graph.

At this point, I had ran out of all other options, so I ran SWAN with a profiler. I had resisted using a profiler so far because I just did not have it set up — I had initially installed the Community Edition of IntelliJ IDEA. I looked at the different graphs offered by IntelliJ. The flame graph and the call tree ended not being that useful. The graph that was useful was the method list, which shows the number of samples in which a method and it’s callees show up. This showed that DDG queries showed up in 95 percent of samples during call-graph construction. Those less that 2 second queries were adding up!

Looking at the code for DDG queries, to decide reachability from one node to another, the it would compute the shortest path between those nodes. This felt a little bit odd, since I would have used a BFS or DFS search, but it wasn’t the end of the world! However, when I looked at the profiling data again, it showed that almost all of the query time was being spent computing shortest paths.

As a first attempt at a fix, I tried to cache the result whenever we found that a node was reachable from another. While this improved the performance a little bit, it was not the massive gains I was looking for. While the cache could answer very quickly when a was reachable from another, it could not answer very quickly when a node was not reachable from another.

My final fix was to precompute the transitive closure of the DDG after it was generated. This way both reachability and unreachability could be decided very quickly by just checking if an edge exists in the closure. Running the code on the 5 minute entry point gave me a run time of less that a second, so the performance was improved by over 3000 times.

Adversarial Input

So what does “adversarial input” have to do with any of this? When the code was written, DDG queries were expected to be very rare. Calling a library function for shortest path was the easiest way to decide reachability — it only took around three lines of code. But the input we were giving SWAN required lots of DDG queries. The algorithm was working as intended, it was just never intended to handle these kind of inputs.

While we got ride of one kind of adversarial input, we have introduced others! Computing the transitive closure of a graph can potentially creates lots and lots of edges in a graph if there are long chains in the graph. This can create a some memory pressure. We haven’t run into this yet, but if we do, this will have to get fixed is some way.

References

1. David F. Bacon and Peter F. Sweeney. 1996. Fast static analysis of C++ virtual function calls. In Proceedings of the 11th ACM SIGPLAN conference on Object-oriented programming, systems, languages, and applications (OOPSLA ’96). Association for Computing Machinery, New York, NY, USA, 324–341. DOI:https://doi.org/10.1145/236337.236371

As stated in my last post, I’ve been working on a toy compiler. One thing that good type-checkers in compilers do is give you helpful suggestions when it fails to type-check. In this post I want to talk about the type-checker suggesting spelling corrections for you. The following is an example of the OCaml REPL suggesting a spelling correction for you.

# let foo x = x + 1;;
val foo : int -> int = <fun>
# boo (2 + 1);;
Error: Unbound value boo
Hint: Did you mean foo?

Let’s take a look at how the compiler implements this! You’ll find the spellcheck function in utils/misc.ml [link]. The function spellcheck in turn uses the edit_distance [link] function. The edit_distance function is the standard dynamic programming solution to computing edit distances.

If you are anything like me, you wouldn’t write dynamic programming code unless it was absolutely critical. I find dynamic programming to be aesthetically unpleasant, and you’d need to pay me to write code like that. There’s also no good way do early cut-off without making the code even more complicated. Is there a way around dynamic programming? Fortunately yes!

Levenshtein Automata

With some quick Googling of “Levenshtein edit distance” and following links in Wikipedia you’ll run into the Wikipedia page for Levenshtein Automaton. “A Levenshtein automaton for a string w and a number n is a finite state automaton that can recognize the set of all strings whose Levenshtein distance from w is at most n.” As we will see below, thankfully, constructing the Levenshtein automaton does not involve dynamic programming. This is almost what we want, if take a look at the spellcheck function, you’ll see that it suggests strings with the best edit distance, so we not only want to know that the edit distance is less than some k, but want to also rank the strings by their edit distance.

Below I will discussing recovering edit distances from Levenshtein automaton. But first a tangent and a bit of a rant!

A Tangent: Thoughts on Automata from a PL Perspective

I find it a little odd that when studying Automata Theory, finite state automata/machines (FSA/FSM) are almost always treated as accept/reject gadgets (see below for thoughts on finite state transducers). The accept/reject versions do have a richer theory in some sense. You have more operations available to you for composing them. Operations such as concatenation and Kleene star make more sense in this setting. But from a PL perspective, it is very limiting to be only working with gadgets that map strings to the set {accept, reject}.

Automata Theory also studies finite state transducers (FST) which map strings in an input alphabet to strings in the output alphabet. But using FSTs as maps from strings to single character strings in the output alphabet gets hairy really quickly. You start to require sentinel end of input characters or more non-determinism. For these use cases, it is much nicer to think of FSM as maps from input strings to their final states. For operations, you still have access to the union and intersection operations, but the programmer has decide what the final states mean after these operations — the theory doesn’t automatically dictate this to be {accept, reject}.

It also feels odd to compute which state the FSA ends up in, and then throw away that information. For Levenshtein Automata, it turns out that states of Levenshtein Automata carry the edit distance of strings, throwing this away feels stupid!

Recovering Edit Distances from Levenshtein Automaton

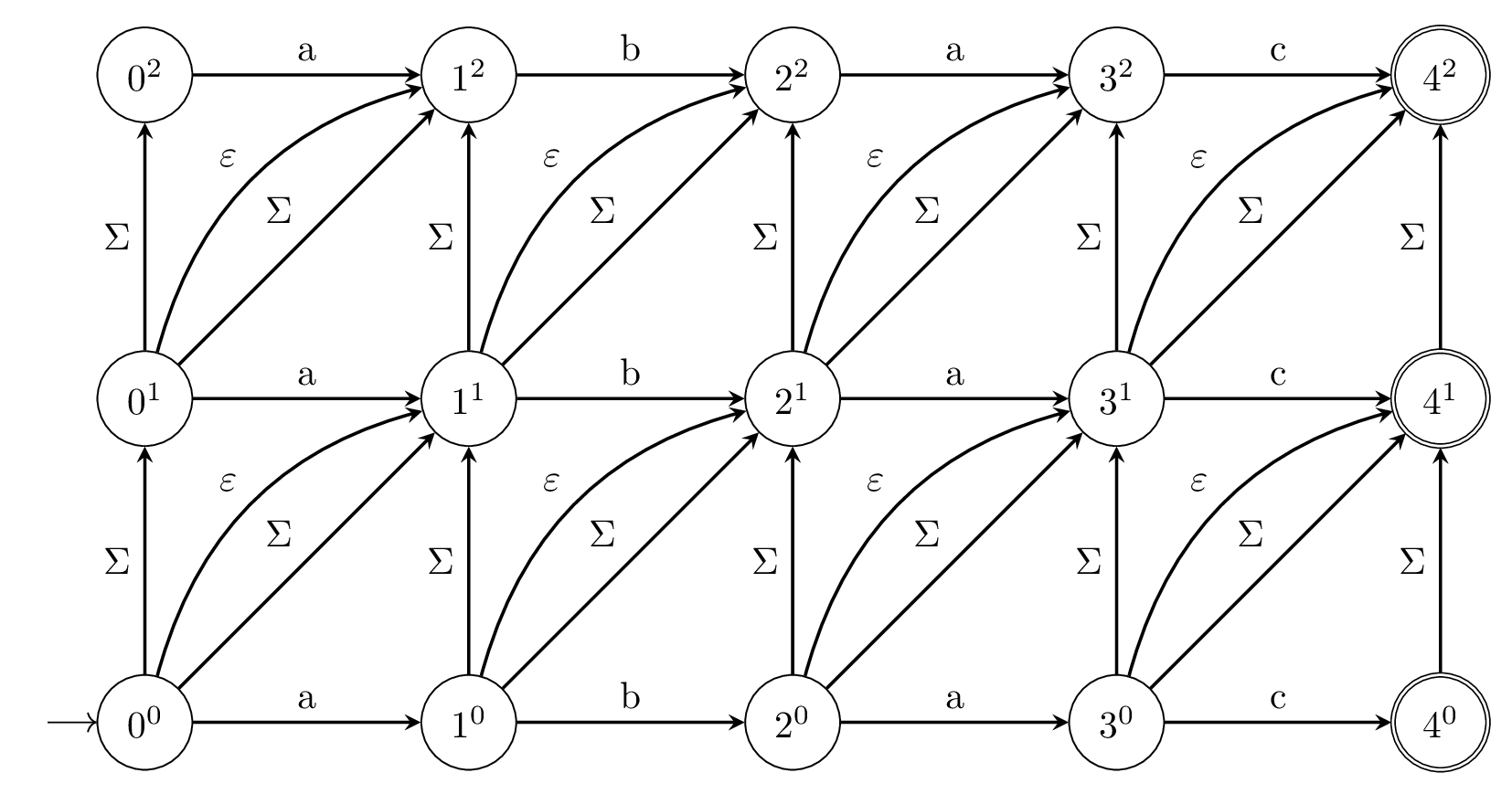
Below is a diagram of the non-deterministic Levenshtein Automaton for the word “SALAD” from the paper by Touzet [1]. The paper uses $k$ to indicate the maximum edit distance that will be matched by the automaton, and in the diagram below $k = 2$.

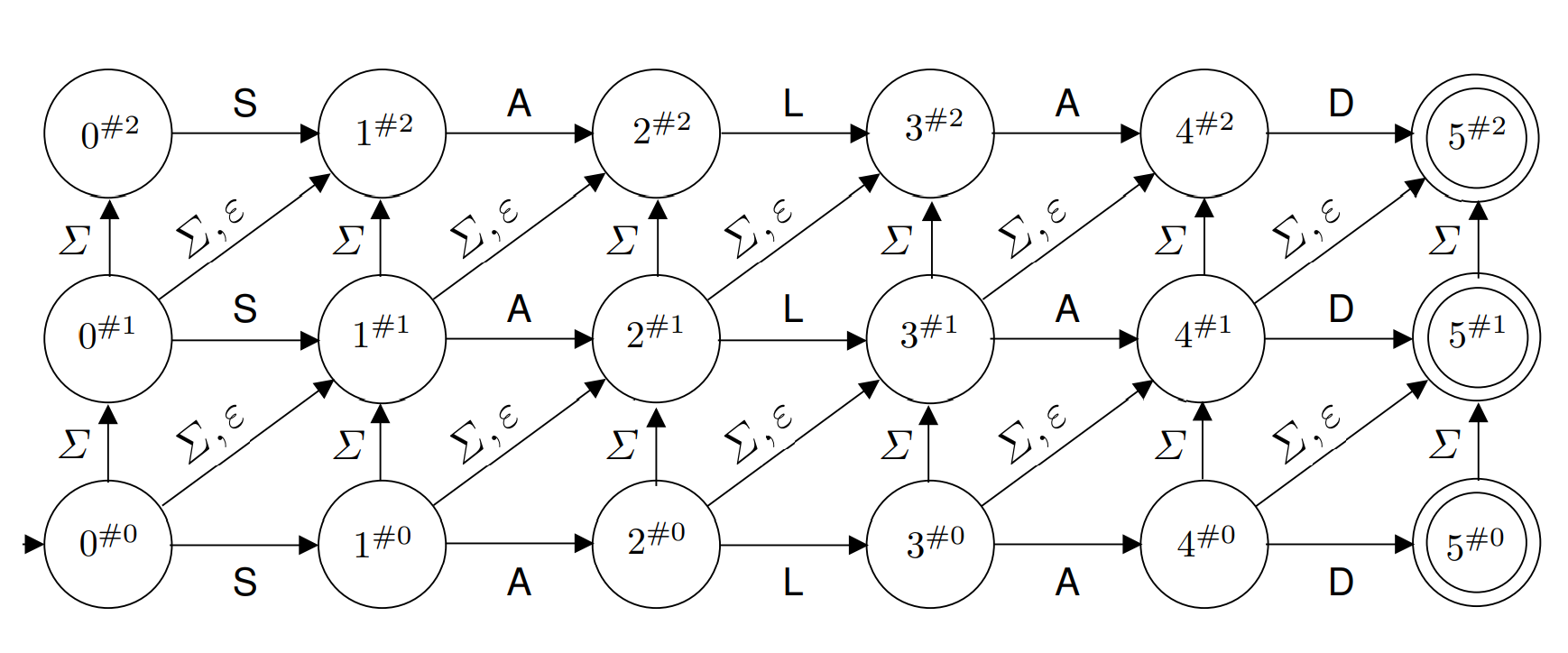
In the diagram above the notation $i^{\#x}$ stands for “$i$ characters have been read in the pattern and $x$ errors have been recorded” [1]. “Horizontal transitions represent identities, vertical transitions represent insertions, and the two types of diagonal transitions represent substitutions ($\Sigma$) and deletions ($\varepsilon$), respectively” [1].

It should immediately jump out to us that since the states of the automaton are labeled with error counts the final states are therefore labeled with edit distances! If we enter multiple final states, the minimal error count will be the edit distance. So if we were using the Levenshtein Automaton for filtering words, we can use the labels to rank strings by their edit distance!

Using Levenshtein Automata, we can get away from dynamic programming. But even this has it’s problems!

Problems Levenshtein Automaton

First, a matter of aesthetics! I wanted to get get away form dynamic programming because I find it aesthetically unpleasant, but I find computing $\varepsilon$-closures to be just as unpleasant. $\varepsilon$-closures also make it difficult to predict behaviour at runtime, but this can be avoided by converting the non-deterministic finite-state automaton (NFA) into a deterministic finite state automaton (DFA).

I haven’t read the paper by Schulz and Mihov [2], but from the diagrams and a quick cursory read through some of the definitions it seems some of this can be mitigated with their subsumption triangles. In fact, one of their results (Theorem 1) is that you can create a Deterministic Levenshtein Automaton for a word $W$ which has size linear in $\left|W\right|.$

But still… The size of the automaton being dependent on the word is a little annoying. As stated above, we may want to compute the DFA from the NFA, and if we do this for large words, we’ll have to store a large DFA in memory.

This is where Universal Levenshtein Automaton come in!

Universal Levenshtein Automaton

Touzet [1] describes Universal Levenshtein Automaton in a fairly accessible way, although some of the ideas presented are derived from the work of Schulz and Mihov [2]. I recently followed the Touzet paper and implemented Universal Levenshtein Automata in my library mula (https://github.com/ifazk/mula/). The paper is a really nice read, but I’ll explain some of the implementation details in mula below.

Suppose we fix a string $P$ of length $m$, and a maximal edit distance $k$. Conceptually, we will be working with an encoding $P'=\$^kP\$^{2k}$, where $\$$ is a sentinel character. We will be comparing $P$ against a word $V$, and we assume that $V$ has size $n \leq m + k$. Again we will be conceptually be working with an encoding $V'=V\$^{m-n+k}$, i.e. $V'$ has size $m+k$.

Bit vectors

The first piece of machinery we will need are characteristic bit vectors. For a character $c$ and a string $S$ of length $i$, the characteristic bit vector $\chi(c,S)$ is a bit vector of length $i$ such that the $j$-th character of the bit vector is $1$ if $S[j]=c$ and $0$ otherwise. For example, $\chi(a,baddy)=01000$, $\chi(d,baddy)=00110$, $\chi(d,bad\$\$)=00100$, and $\chi(\$,baddy)=00000$.

For an index $i$ (the paper uses 1-indexing), we will have to compute $\chi(V'[j],P'[j .. j+2k])$. In my implementation I split this up into two cases, first where $j\le n$, and a second where $n < j \le n+k$.

For $j\le n$, this is just $\chi(V[j],P'[j .. j+2k])$, it’s a character from $V$.

1. We can compute the number $\$$ in the prefix of $P'[j .. j+2k]$ as $a=\min(0,k + 1 - j)$.
2. The overlap between $P'[j .. j+2k]$ and $P$ is $P[b,c]$ for $b=\max(1,j-k)$ and $c=\min(j+k,m)$.
3. We can compute the number $\$$ in the suffix of $P'[j .. j+2k]$ as $d=\min(0,k + 1 - j)$.
4. So $\chi(V[j],P'[j .. j+2k])=0^a \cdot P[b,c] \cdot 0^d$.

For $j> n$, we can follow similar steps to get $\chi(\$,P'[j .. j+2k])=1^a \cdot 0^{c+1-b} \cdot 1^d$.

Note: There is a typo in the Touzet paper in Definition 2. The paper asks us to compute $\chi(V'[j],P'[j-k .. j+k])$, but this is undefined when $j<k$.

Non-deterministic Universal Levenshtein Automata

Below is a diagram of the non-deterministic Universal Levenshtein Automaton for $k=2$ (shamelessly stolen from Touzet [1] again). It transitions on the bit vectors from the above.

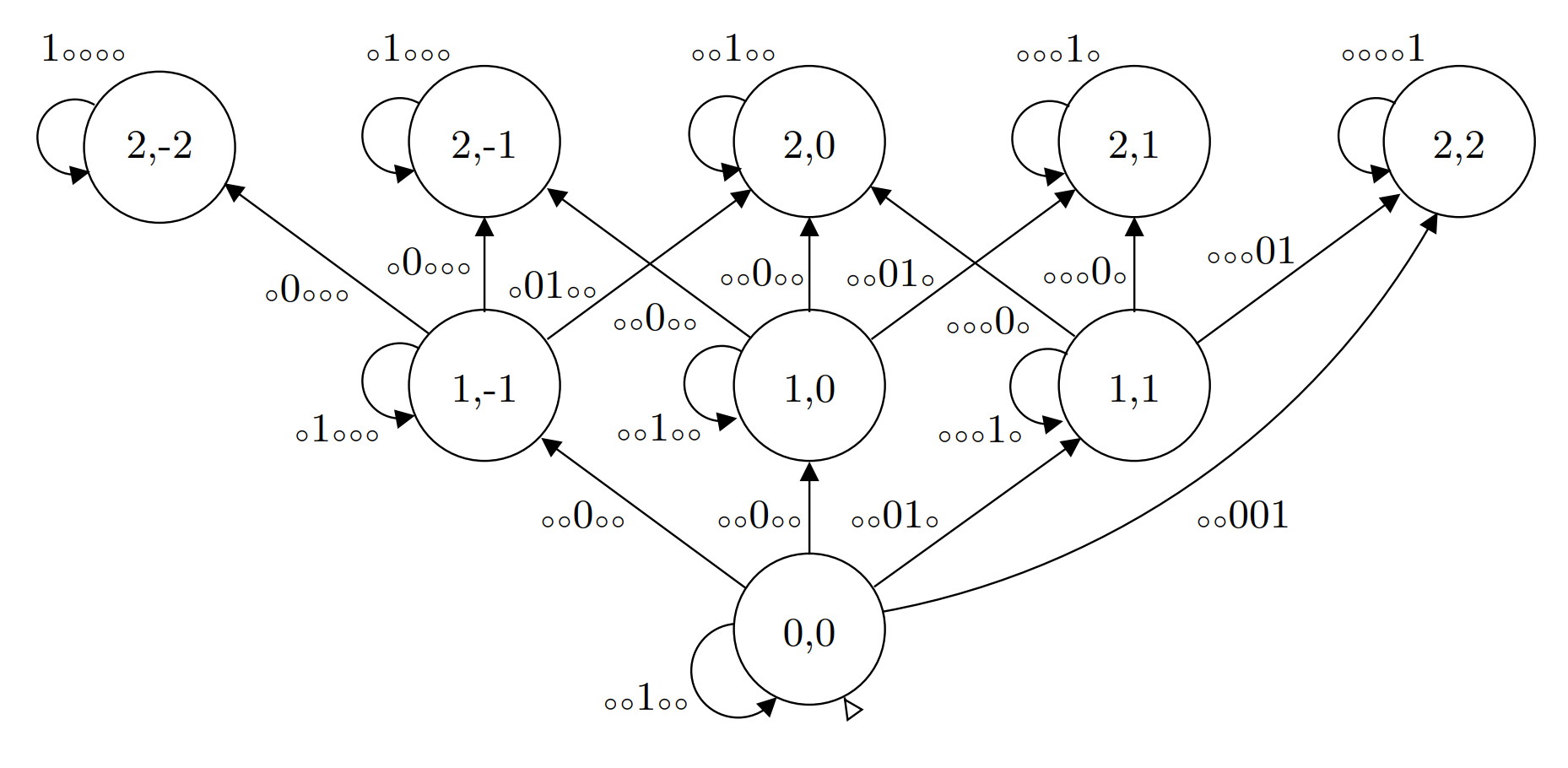
Transitions to the left are delete edits, transitions to the right are insert edits, and transitions upward are substitution edits. Supposed $j$ characters have been fed into the automaton. The labels $(x,y)$ should be read as “$x$ errors have been recorded, and to keep the same number of errors, the $j+1$-th of $V'$ character must be the same as the $j+1-y$-th character of $P\$^{k}$”.

The paper details a subsumption relation, so any state $(x,y)$ subsumes states in the triangle above it. For example, in the diagram above $(1,0)$ subsumes $(2,-1)$, $(2,0)$, and $(2,1)$. This means that after transitioning from a set of states to another set of states, we can prune any subsumed states. After pruning, there is a bound on how many states can be active in the automaton, and it is $2k+1$. The pruning is implemented in mula.

The Nice Parts of Universal Levenshtein Automata

Firstly, it gets rid of my last aesthetic complaint. We no longer have $\varepsilon$-transitions!

Secondly, the automata are independent of input strings, they only depend on $k$.

Thirdly, the NFA is easily computable. Given an input state and a bit vector, we can easily compute its transition. If we are in lane $y$, and the $(k+1)+y$-th element of the bit vector is $1$, then we stay in the same state. Otherwise, we make insert and substitution and delete transitions if possible. For insert and substitution transitions, the current error count must less than $k$. For delete transitions, we look for the first bit in the bit vector to the right of the lane that is $1$, and transition to that delete state. If all the bits to the right are $0$, there will not be a delete transition. Here, right of the lane means the bits starting at the $(k+2)+y$-th bit of the bit vector.

Fourthly, the bound on states being $2k+1$ is really nice. Without the subsumption relation, the number of states at any given time could be quadratic in $k$, but in Universal Levenshtein Automata it is linear in $k$.

Lastly, we still have the nice property that states carry error counts.

What’s Missing from mula?

I only implemented matching with NFAs in mula. It should be possible to pre-compute the DFA’s for up to $k=3$ and ship them with the library.

It should also be possible to add other types of Levenshtein Automata to mula. For instance, in optical character recognition, it is useful to count splitting a character into two and merging two characters into one as single edits.

I currently have matching with the NFA, but there are use cases (e.g. suggestions in IDEs) where knowing exactly what has been matched is useful. I would like to additionally provide Finite State Transducers which output $1$ if we transition to the same state, and $0$s when we transition to states with higher errors.

Conclusion

Universal Levenshtein Automata are really nice, and simple to implement! They allow you to avoid annoying programming like dynamic programming and computing $\varepsilon$-closures. If you don’t care about actual full edit distances, and only care about distances up to a limit, Universal Levenshtein Automata are probably what you want!

References

1. Hélène Touzet. On the Levenshtein Automaton and the Size of the Neighborhood of a Word. LATA2016 - 10th International Conference on Language and Automata Theory and Applications, Mar 2016, Prague, Czech Republic. pp.207-218, 10.1007/978-3-319-30000-9_16.
2. Klaus U. Schulz and Stoyan Mihov. Fast string correction with Levenshtein automata. IJDAR - International Journal on Document Analysis and Recognition volume 5, pages 67–85 (2002). 10.1007/s10032-002-0082-8

Further Readings

Levenshtein Automata in Python: A blog post about implementing Levenshtein Automata in python.

Lucene FuzzyQuery: This is a blog post about how this was implemented in Lucene. Using Python to generate a Java file really feels like a crime!

Levenshtein Automata in spelll: This is an implementation of Levenshtein Automata in OCaml. It follows a different implementation in Python.

Proofs about Universal Levenshtein Automata: This thesis proves some properties of Universal Levenshtein Automata. I have not read the thesis, but did use Figure 9 to implement Demarau-Levenshtein Automata (restricted edits) in mula.

Recently I have been working through a compiler book on the side, and there were two places where I wanted custom types but did not want to define them globally. The types were going to be used locally within a function, and it felt odd to define them globally when no other function was going to use them. Even defining them locally in the same file and then then hiding it in the interface file felt odd, I just needed the types for single functions, nothing else in the module!

This is what I mean by Conjuring Types from the Ether: having access to types without having to declare them! Generally you want lightweight syntax for creating values of these types, otherwise it would be worth the effort to declare them.

Both the places where I had the problem are simply cases of Boolean Blindness, and both stem from me trying to keep pattern matching simple!

Boolean Blindness

The first case where I wanted to conjure types from the ether is a more classic version of Boolean Blindness. I had some code like this:

let global_function_exposed_in_module params =
  ...
  let check_function args = ... in
  match check_function params with
  | true -> ??
  | false -> ??

As I was trying to fill in the above ??, I realized that I had forgotten what true meant and what false meant. And the actualy nome of check_function was weird enough that I couldn’t figure out if true meant success or not, check_function is just a place holder name I’m using for this post.

This is exactly Boolean Blindness! As Bob Harper put it I have “blinded” myself by “reducing the information” I had “at hand to a bit, and then trying to recover that information later by remembering the provenance of that bit”.

The JavaScript/TypeScript Solution: At this point, if I were using a in a language like JavaScript, I would go and modify check_function to return the strings "Success" or "Fail". This is somewhat natural in JavaScript because you can case match on strings. TypeScript with it’s literal types improves things! The case match on "Success" and "Fail" would be compile time checked to be exhaustive! (Disclaimer: I haven’t actually checked if literal types can be conjured from the ether or not.)

The Racket/Lisp Solution: In Racket, or any Lisp with pattern matching, the situation is ever so slightly improved because you have access to symbols. You can return the symbols 'Success or 'Fail, and the situation is again improved by using typed racket for exhastivity checking. But overall this is very similar to the JavaScript/TypeScript case.

The OCaml Solution: I was programming in OCaml, and I was really happy that OCaml has something similar to symbols, called Polymorphic Variants. Generally, Polymorphic Variants can carry around data other pieces of data just like like Algebraic Data Types, and have interesting structural subtyping between themselves. These properties weren’t that useful to me, but what was useful was being able to conjure the Polymorphic Variants from the Ether without having to declare them globally.

let global_function_exposed_in_module params =
  ...
  let check_function args: [`Success|`Fail] = ... in
  match check_function params with
  | `Success -> ??
  | `Fail -> ??

The use of the type [``Success|``Fail] is contained completely within this function, and I also get a exhaustivity check!

Position Blindness?

This second case where I wanted to conjure types from the other involved tuples and records. I was traversing the AST, and creating sets of two kinds of variables. Initially my code looked like the following, collect_exp, and collect_dec are mutually recursive.

  let collect_exp (env: (var Set.t * var Set.t)) params:
    var Set.t * var Set.t =
    ...
  and collect_dec (env: (var Set.t * var Set.t)) params:
    var Set.t * var Set.t =
    ...
    let (collect_a?, collect_b?) = collect_exp args in
    ...

Midway through collect_dec I forgot what kind of variable collect_exp returned in which position. Normally, would know which position is what based on the differences in the types in the two positions, but here both the types are the same.

This again is another kind of boolean blindness. To illustrate this, I’m gong to switch to Standard ML syntax.

    let x = collect_exp args in
    let collect_a = x#1? in
    let collect_b = x#2? in
    ...

To choose between variable kind a and variable kind b, I am relying on the boolean 1|2!

The solution here in an untyped setting is to modify the code to use dictionaries/records instead of tuples. So collect_exp would return {kind_a: var Set.t, kind_b: var Set.b}. We are no longer blind to any positions, because we have names instead, just like names in variants/symbols.

But declaring a type like the following feels overkill.

type record_used_in_foo_function_only =
  { kind_a: var Set.t
  ; kind_b: var Set.t
  }

In OCaml, you can conjure object types from the ether, but the syntax there is a little heavy weight. For example, here’s how you would create an object representing the above record.

let my_object =
  object
    val kind_a = Set.empty
    val kind_b = Set.empty
  end

I consider the use of the keyword object and the delimiter end to be fairly heavy. Plus they cannot be easily destruct like tuples and records, and copy syntax for objects is also somewhat ugly. For records you can do { x with kind_a = Set.union y z }.

In the end, I ended up just keeping the code as is and just going back to collect_exp to figure out which position is what, but I really wish I could conjure a record type from the ether. This is possible in other languages. The examples I can think of easily right now are records in Flix and Elm. In these languages you can destruct records with types conjured from the ether using record style patern matching, and they also have lightweight copy syntax.

let {kind_a = y; kind_b = z} = collect_exp args in

An aternative that I did consider but then decided against is changing the tuples to contain polymorphic variants.

let collect_exp env params: ([`A of var Set.t], [`B of var Set.t]).

As I mentioned above, polymorphic variants can carry data, and here the variant `A caries a variable set with it.

Position Blindness in Function Arguments

This kind of positional blindness also happens when passing arguments to functions of the same type. For example, I can never remember which of the arguments of memcpy is the source and which is the destination without looking at the manpage. The declared type is memcpy(void *, void *, size_t).

Most modern languages solve this by using named arguments. Some languages like (iirc) Swift, are strict about not letting you pass named arguments positionally, but other languages like C# allow for flexibility. Alternatively, you can also ask that the arguments be records or structs. E.g. what if the argument to memcpy(MemCpy) was a struct?

typedef struct {
  void * dest, src;
  size_t size;
} MemCpy;

Posting this mostly for my personal use, but it might be helpful for others.

For some reason, I have been having trouble visiting the HOPL-I webpage. I used the the Wayback Machine to find the folowing useful links:

• Recent archive of the HOPL-I webpage
• HOPL-I Conference Proceedings

I’m looking forward to reading the papers on ALGOL, SIMULA, BASIC and LISP, but we’ll see how far I get. There is the never ending problem of higher priority things being added to my reading list, so this kind of recreational reading often falls by the wayside. Might also try to sneak the FORTRAN and APL papers into my reading list.

The HOPL-I book might also be interesting, since it also contains transcripts of the presentation, questions (with some questions having additional answers by the authors), and summaries of the languages. There are more datails in the conference webpage, so I would highly encourage everyone to visit the conference page or its archived version first.

It’s been a couple years since my post A JavaScript-free Hakyll site. Today I got an email from someone asking for some help setting up their own JavaScript-free Hakyll site.

The approach in that post is really slow! Most of the slowdown is from the following piece of code.

readCreateProcess (shell $ kaTeXCmd mt) inner

We take a single String called inner, create a $\KaTeX$ cli process, feed inner to the process’ standard input, read the converted string from its standard output, and then close the process.

At the time I did not realize how slow creating a new processes for every piece of $\LaTeX$ in your code would be. My thought process was something like this: “It’s been a million years of Operating Systems research, starting the same process over and over again should not be that bad.” Afterall, I do this all the time with Unix tools. But I started to feel the slow down at around 3 files containing $\LaTeX$.

ZMQ IPC to the Rescue!

I updated my site to use a single $\KaTeX$ process which runs as a server, and talks to Hakyll over ZMQ.

Here is the JavaScript code.

const katex = require("katex");
const zmq = require("zeromq");

async function run() {
    const sock = new zmq.Reply;

    await sock.bind("ipc:///tmp/katex");

    for await (const [msg] of sock) {
        let msgObj = JSON.parse(msg);
        let latex = msgObj.latex;
        let options = msgObj.options;
        options.throwOnError = false;
        let html = katex.renderToString(latex, options);
        console.log(`Recieved\n${msg}`);
        console.log(`Sending\n${html}`);
        await sock.send(html);
    }
}

run();

Here is the updated Haskell code.

{-# LANGUAGE OverloadedStrings #-}
{-# LANGUAGE DeriveGeneric #-}

module KaTeX.KaTeXIPC
    ( kaTeXifyIO
    ) where

import Control.Monad
import System.ZMQ4.Monadic
import qualified Data.ByteString.Char8 as BS (putStr, putStrLn)
import Data.ByteString (ByteString)
import Data.ByteString.Lazy (toStrict)
import GHC.Generics
import Data.Text
import Data.Text.Encoding (decodeUtf8)
-- Pandoc
import Text.Pandoc.Definition (MathType(..), Inline(Math, RawInline), Pandoc, Format(..))
import Text.Pandoc.Readers.HTML (readHtml)
import Text.Pandoc.Options (def)
import Text.Pandoc.Walk (walkM)
import Text.Pandoc.Class (PandocPure, runPure)
-- Aeson
import Data.Aeson hiding (Options)

--------------------------------------------------------------------------------
-- DataTypes
--------------------------------------------------------------------------------
newtype Options = Options
  { displayMode :: Bool
  } deriving (Generic, Show)

data TeXMath = TeXMath
  { latex :: Text
  , options :: Options
  } deriving (Generic, Show)

--------------------------------------------------------------------------------
-- Instances
--------------------------------------------------------------------------------
instance ToJSON Options where
  -- No need to provide implementation (Generic)
instance FromJSON Options where
  -- No need to provide implementation (Generic)
instance ToJSON TeXMath where
  -- No need to provide implementation (Generic)
instance FromJSON TeXMath where
  -- No need to provide implementation (Generic)

--------------------------------------------------------------------------------
-- Convert Inline
--------------------------------------------------------------------------------
toTeXMath :: MathType -> Text -> TeXMath
toTeXMath mt inner =
  TeXMath
  { latex = inner
  , options = toOptions mt
  }
  where
    toOptions DisplayMath = Options { displayMode = True }
    toOptions _ = Options { displayMode = False }


toKaTeX :: TeXMath -> IO ByteString
toKaTeX tex = runZMQ $ do
  requester <- socket Req
  connect requester "ipc:///tmp/katex"
  send requester [] (toStrict $ encode tex)
  receive requester

parseKaTeX :: Text -> Maybe Inline
parseKaTeX txt =
  -- Ensure txt is parsable HTML
  case runPure $ readHtml def txt of
    Right _   -> Just (RawInline (Format "html") txt)
    otherwise -> Nothing

kaTeXify :: Inline -> IO Inline
kaTeXify orig@(Math mt str) =
  do
    bs <- toKaTeX (toTeXMath mt str)
    case (parseKaTeX $ decodeUtf8 bs) of
      Just inl -> return inl
      Nothing  -> return orig
kaTeXify x = return x

--------------------------------------------------------------------------------
-- Convert Pandoc
--------------------------------------------------------------------------------
kaTeXifyIO :: Pandoc -> IO Pandoc
kaTeXifyIO p = do
  walkM kaTeXify p

I recently attended the SPLASH-E presentation on Lambdulus: Teaching Lambda Calculus Practically by Jan Sliacky and Petr Maj. It was a very interesting presentation describing the Programming Paradigms (PPA) course at the Czech Technical University. I really think they are onto something!

Much of the presentation focused on the web-based programmer-friendly λ-calculus evaluator, affectionately called Lambdulus. To make the evaluator more programmer-friendly, they extend the untyped λ-calculus with macros and break-points and they use special evaluation rules for reducing macros. The paper was also a very good read and went into a little more detail about the course and their approach to teaching the λ-calculus.

One of the more important parts of Lambdulus is that it chooses which type of evaluation is appropriate. This is particularly important for reducing church numerals, but also leads to much cleaner looking λ-expressions because they are careful with how they expand macros. Lambdulus is also careful about how many of the evaluation steps to show to the programmer.

Macros are named expressions defined using the syntax NAME := [λ-expression]. Lambdulus is very careful about when they expand macros. In general, macros are only expanded if they are applied to some other expression. If a λ-abstraction is applied to a macro it is passed by reference, i.e. the abstracted variable is substituted for the macro not its definition. This makes the reduced expression look much cleaner.

Lambdulus also supports something they call dynamic macros. Currently these are numbers and arithmetic operators. Instead of defining a infinitely many macros manually, one for each church numeral, Lambdulus defines numeric macros dynamically. Reduction, when arithmetic operators are applied to numeric macros are also simplified.

Overall I really liked the project and their approach to teaching students how to program in the λ-calculus! I really liked how they have a clearly defined goal of teaching students how to program in the λ-calculus by treating it as a “real” programming language and they build everything around that goal. One of the strengths of their approach is realizing that when programming in the λ-calculus, we really want different kinds of reduction for different kinds of λ-expressions. For example, even if we are working in a call-by-value or call-by-name setting, for arithmetic on church numerals we probably want to be a little more agressive and do a full normal order reduction and then contract the result into a numeric macro. This makes the result look a lot cleaner and helps programmers debug their λ-calculus programs since what is going on during execution is a lot more clearer.

Their evaluator is available at https://lambdulus.github.io/! They paid a lot of attention to making Lambdulus more developer friendly. I didn’t talk about break-points above, but I found that interesting as well! I remember having a lot of trouble with church encodings when I was learning to program in the λ-calculus and I really think I could have benefitted from playing around in Lambdulus!

Background Required: This post assumes some familiarity with the simply typed $\lambda$-calculus and $\beta$-reduction.

Pure Type Systems

Pure Type Systems (PTS) are a class of explicitly typed $\lambda$-calculi. The most remarkable thing about PTSs, is that types, terms, kinds are all expressed in one syntax and with only a few simple rules they can express crazy type systems.

The general system is defined as being polymorphic over three sets: a empty set of sorts $S$, and the set of axioms $Ax$ and the set of rules $R$, where $Ax$ contains pairs of sorts and $R$ contains triples of sorts. By selecting various $S, Ax, R$ we can express different $\lambda$-calculi.

The simply typed $\lambda$-calculus (STLC) can be viewed as a Pure Type System, but this system has some interesting (and sometimes annoying) properties. In this post, I will highlight some of these properties.

STLC as a Pure Type System

The typing rules for Pure Type Systems are usually expressed in their most general setting, having rules that can express dependent types and type level computation. These are not necessary to study the STLC, so in what follows we only express the rules necessary to express simple types and expressions.

In the following, the set of sorts is $S = \{\square{},*\}$, $s$ ranges over sorts, $x,y$ and $X,Y$ ranges over variables, and $a,b,c,f$ and $A,B,C,F$ range over terms.

Type Variables as Base Types

When studying the non-PTS STLC, we usually assume a set of base types. In the PTS version of STLC, we instead assume a base kind $*$ and allow the introduction of type variables as base types of kind $*$.

$$\begin{array}{c} \vdash *:\square{} \end{array}\quad(\text{Axiom})$$

$$\begin{array}{c} \Gamma \vdash A : s \\ \hline \Gamma, x:A \vdash x : A \end{array}\quad(\text{Start})$$

$$\begin{array}{c} \Gamma \vdash A : B \qquad \Gamma \vdash C : s \\ \hline \Gamma, x:C \vdash A : B \end{array}\quad(\text{Weakening})$$

Here the $(\text{Axiom})$ rule can be read as “$*$ is a kind”.

The $(\text{Start})$ rule is used in two ways. Firstly, it allows for typing judgements of the following form which can be roughly read as “$x$ is a new base type”.

$$\Gamma, X:* \vdash X : *$$

Secondly, it allows us to introduce variables of base types into the context.

$$\Gamma, X:*, x: X \vdash x : X$$

The $(\text{Weakening})$ rule allows us to type terms in extended contexts.

Function Types

The rules so far, only allow us to work with types of the form $X:*$. The next rule allows us to work with function types.

$$\begin{array}{c} \Gamma \vdash A : * \qquad \Gamma \vdash B : * \\ \hline \Gamma \vdash A \to B : * \end{array}\quad(\text{Product})$$

Using the above rule we can get typing judgements such as the following.

$$\Gamma, X:*, Y:*, x: X \to Y \vdash x : X \to Y$$

$\lambda$ Abstractions and Applications

The next rules are somewhat standard and allow us to type $\lambda$ abstractions and applications.

$$\begin{array}{c} \Gamma,x:A \vdash a : B \qquad \Gamma \vdash A \to B : * \\ \hline \Gamma \vdash \lambda (x:A).a : A \to B \end{array}\quad(\text{Abstraction})$$

$$\begin{array}{c} \Gamma \vdash f : A \to B \qquad \Gamma \vdash a : A \\ \hline \Gamma \vdash f\,a : B \end{array}\quad(\text{Application})$$

The above are all the rules we need to study the PTS version of the simply typed $\lambda$ calculus. The system we presented does not have any type-level abstraction or computation, so some PTS rules were elided.

Interesting Facts

1. No Elimination Rule for Type Variables

One of the wierder quirks of the PTS version of STLC is that there are no Elimination rules for type variables. This means that the only thing that we can type in the empty context is $\vdash * : \square$. Everything else must be typed in a non-empty context.

$$\begin{array}{c} X:* \vdash \lambda (x:X).x : X \to X \end{array}$$

Although, there are no “closed” terms, we can still define $\beta$-reduction and prove progress and preservation lemmas, they just must happen in non-empty contexts. This brings us to our second interesting fact.

2. Progress Lemma has an Additional Special Case

The progress lemma for the non-PTS STLC is stated as follows.

Lemma (non-PTS Progress): For any $\Gamma\vdash A : *$, either $A$ is a variable, a $\lambda$-abstraction, or there exists a term $B$ such that $A\to_{\beta}B$.

The PTS version has an additional special case, since sorts are treated as first class and are an additional normal form in PTS.

Lemma (Progress): For any $\Gamma\vdash A : *$, either $A$ is a variable, a $\lambda$-abstraction, $A$ is a sort, or there exists a term $B$ such that $A\to_{\beta}B$.

3. Only Allow Types and Sorts in Contexts

This is not specific to STLC, but to applies to any PTSs. To introduce any binding of the form $x:A$ into the context, we must first show that $A:s$ for some sort $s$.

4. Still Simply Typed!

While the PTS version of STLC has type variables, non-type/non-sort terms are still simply typed. We still do not have any form of polymorphism, type constructors, or dependent types. We also do not have any kind of recursion.

Conclusion

The fact that there are no typable closed terms other than $*$ is somewhat weird, but it stems from the fact that we do not want $\lambda$-abstractions which are polymorphic over types when studying STLC. This makes the PTS version of STLC somewhat uninteresting. However, there are many interesting extensions of the PTS version of STLC. For example, we can introduce an additional axiom $\vdash Nat:*$ and constants $0$ and functions $succ,pred$ to study PCF in a PTS setting. We can also consider the above system extended with simple inductive types, which we will explore in a future post!